[研究分野について]

リー群の表現について研究しています。対称性は数学や自然科学の様々な場所に現れ、対称性を利用することは強力な手段になります。数学では対称性は変換群の作用として捉えられます。群の表現とは群のベクトル空間への作用、つまり対称性付きのベクトル空間のことです。線形代数はあらゆる場面で必須の道具になっていますが、群作用付きの対象を研究する上では群の表現についての理論がそのような基本的な役割を果たすと言えるでしょう。例えば多様体が与えられると、その上の関数空間、微分形式のなす空間、より一般にベクトル束、層の切断の空間、あるいはコホモロジーなどのベクトル空間を考えることができますが、群作用つきの設定では群の表現を得ることになります。逆に、群からスタートしてその表現を研究するという立場から見ても、群の作用する多様体を考えてそこから表現を得るというのは基本的な方法になります。

リー群とは群に多様体の構造が入っているもので、たとえば回転対称性などの連続な変換を扱うものです。サイズnの可逆行列全体のなす群GL(n)などがその典型例です。群は数学に現れる対称性を抜き出した抽象的な概念とも言えますが、一方で古くから研究されてきた具体的な特殊関数や積分変換などもリー群の作用を用いて再解釈できます。古典的によく理解されていた話の背後には、しばしば群の作用が隠れているということがあります。

同じ表現が数学の異なる分野に現れるということは、様々な方向から同じところに到達できるということでもあり、自分の好きな分野から研究することができます。実際、表現論の歴史を振り返っても、数理物理、保型形式論、代数解析など他の分野と互いに深く関わりあいながら豊かに発展してきました。表現を通して分野横断的に数学を視ることができるのも表現論の面白さであるといえます。

私自身はリー群の表現や関連する幾何、特に実簡約リー群の無限次元表現の制限や誘導について研究しています。リー群Gとその部分リー群Hがあったとき、Gの表現をHの作用に制限してHの表現が得られる。また逆にHの表現があったとき、Gの表現を得る誘導という操作がある。この制限や誘導という操作による表現の振る舞いを調べるのには多くのアプローチが考えられますが、私は特にD加群による表現の実現および軌道の方法との関連を研究してきました。リー群が多様体に作用しているとき、その上の関数空間にはリー環が微分作用素として作用します。この関数空間への作用の一般化、抽象化として、多様体上のD加群からリー環の表現を得ることができます。リー環の表現と旗多様体上のD加群との間の対応はBeilinson-Bernstein、柏原-Brylinskiによる理論として知られています。この理論により、リー環の表現と旗多様体上のD加群との間に橋がかかりました。この橋を渡って、D加群を通してリー環、リー群の表現論の問題を調べるというのが私のこれまでの研究のアプローチの中心になっています。一方、シンプレクティック幾何（リー環の余随伴軌道）と表現論との間の関係も長く研究されており、軌道の方法と呼ばれています。最近は、軌道の方法を援用して表現の性質を調べることにも興味をもっています。

[これまでの経緯]

次に、これまで私がどのように数学の学習、研究をしてきたかを書きます。これから専攻を決める方にとって何かの参考になればと思います。

大学に入る前

数学について一般向けに書かれた本が好きで読んでいた。たとえば
　『フーリエの冒険』　トランスナショナル・カレッジ・オブ・レックス
　志賀浩二　『数学が生まれる物語、数学が育っていく物語』　
が面白かったことを憶えている。また有名な
　高木貞治 『初等整数論講義』　
　高木貞治 『解析概論』
なども読んでみようと思ったが、少し読んでは考え、わからなかったら何週間か放っておいてまた考えてみるという調子でのんびりやっていてあまり進まなかった。ただ学問としての数学に触れ、恐ろしく広い世界があるのだということを感じた。この頃から漠然と数学の道に進むことを考え始めた。

学部のとき

大学入学前年から学部時代に、近い世代の先輩や同期に誘われて一緒に数学の本を読むセミナーをした。
　森田茂之 『微分形式の幾何学』 岩波講座 現代数学の基礎
　Otto Forster “courses on Riemann Surfaces"
　David Mumford “The Red Book of Varieties and Schemes"
等の本を輪読した。MumfordのRed bookは代数幾何の有名な教科書だが、書かれていることを追うのに精一杯で、可換環論の知識が足りなかったために環論の本を開いてもなかなかイメージがわかないという有様だったが、このときにセミナーをしていたおかげで代数幾何の言葉にある程度慣れることができたんじゃないかと思う。
学部三年のころに、リー環とその表現のスタンダードな教科書
　James Humphreys, “Introduction to Lie Algebras and Representation Theory”
を手に取ってパラパラとめくってみると、

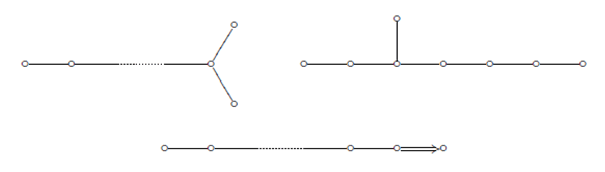
のような図が書かれていた。この図は一体何なんだろうと気になって本を読み始めてみると、非常に読み易くほぼ線形代数だけを使って議論が展開され、半単純リー環というクラスについてはルート系という組み合わせ論的データで構造が明らかになり、分類までできてしまう。さらにその表現もルート系から完全にわかってしまうという見事な話で夢中になって読んだ。この内容はコンパクトなリー群の構造論、表現論とほぼ同じ理論でCartan-Weyl理論と呼ばれている。ひとつの完結した理論であるが、これを手本に様々な方向に表現論が発展している。

ということで学部四年のセミナーは何か表現論の本にしようかと思い、松本久義先生のもとで
　Neil Chriss, Victor Ginzburg, “Representation Theory and Complex Geometry”

を読むことになった。ワイル群の表現やアフィンヘッケ環の表現の幾何学的実現がテーマになっている。当時の自分の知識からすると随分背伸びした本で、表現論をやる前の準備のところで次々に知らないことが出てきて四苦八苦したが、表現論が始まると美しい話が展開されて苦労が報われたように思った。このような方向で、表現の幾何学的実現を通した研究は現在盛んに行われている。

院生のとき

小林俊行先生に師事した。修士一年のときに
　谷崎俊之, 堀田良之, 『D加群と代数群』 シュプリンガー現代数学シリーズ
　(英語版は，Ryoshi Hotta, Kiyoshi Takeuchi, Toshiyuki Tanisaki, “D-Modules, Perverse Sheaves, and Representation Theory”)
を読んでいた。D加群の一般的な理論から始まって、表現論への応用まで書かれている本である。これを読み終えて修士二年になるころに、小林先生からリー群の（無限次元）表現の制限の話を紹介していただいた。
　Toshiyuki Kobayashi, “Discrete decomposability of the restriction of Aq(λ) with respect to reductive subgroups” (1994,1998)
表現を部分群に制限したときにどのように最小単位に分解するかという問題である。分解の様子を具体的に表した式を分岐則という。表現の制限（離散分解性）は小林先生が創始された理論である。一般に無限次元表現の制限は捉えるのが困難で、特別な場合以外ほとんど何もわからないという状況だったが、小林理論により比較的振る舞いの良いクラスが豊富にあるということが明らかになった。結局この良いクラスについての分岐則を求めるというのが修士課程、博士課程の研究の中心テーマになった。

分岐則を調べるにあたって、まずは既に分岐則の公式が知られている場合に、それが対応する旗多様体上のD加群とどのような関係があるかを考えてみた。すると旗多様体の側の軌道の個数と分岐則に現れる系列の個数が同じになっているということに気づき、これが取っ掛かりになった。旗多様体上の局所座標をとってリー環の作用を書き下してみるという原始的な方法で、いくつかの人工的な仮定の下では分岐則の端の部分が捉えられるということがわかった。そのときに一番最後に残ったのがある部分リー環を構成するところで、これを考えていた一、二か月の間は、初めて何か自分にも新しいことができるかもしれないと思って、他のことを全部そっちのけで熱中し寝ている間も考えているような状態だった。その後、証明は単純になって人工的な仮定も外れ、これらの結果をまとめて60ページほどの修士論文を提出した。

修士の結果で分岐則の一部分（端の部分）がわかったものの、完全な式を求めたわけでは無かったため、博士になってからも引き続き分岐則を調べることになる。一方で振る舞いの良いクラスを小林の判定条件を使って分類し、これは小林先生との共著
Toshiyuki Kobayashi, Yoshiki Oshima, “Classification of discretely decomposable Aq(λ) with respect to reductive symmetric pairs”になった。いくつかの例で分岐則の計算をしていると、分類を使ってしらみつぶしに計算すれば全ての場合に公式を求められるだろうという目途が立ってきた。分類を使わない一般的な扱いは思いつかなかったため、90通りほどある全ての場合を一つずつ計算してみることにした。一日ひとつの場合をやれば、三か月程度で終わるはずで、まあそんなに都合よくは進まなかったが、何とかほぼすべての場合を計算し、100あまりの公式ができた。

博士二年の時にドイツのマックスプランク研究所で開かれた二か月ほどの表現論のプログラムに参加した。写真はそのとき初めて海外で講演した時のものである。小林先生と共同で行った分類の結果について紹介した。縦に三枚の黒板があって、上の黒板を下に戻すときは手元のひもを引けばよいのだが、下の黒板を上に戻すときは投げてスライドさせないといけないという仕組みになっている。思い切りが足りないと上まで届かず、勢いが良すぎると跳ね返って戻ってしまうというわけで苦戦していた人もいたので、自分の講演の前日にこっそり練習しておいた。これで準備万端かと思ったら講演が始まると字を書くたびにチョークが折れて動揺した。後から、そのチョークは折って使うのだと言われた。講演自体は成功したようで安心した。

博士修了後

博士を取得した後、東京大学カブリ数物連携宇宙研究機構（カブリIPMU）で研究員をすることになった。数学と物理の研究者が協力して宇宙の謎を解明するという目的で作られた研究所である。私は物理や宇宙に関する知識はほとんどなかったが、物理学者と話すのは大変刺激になった。最先端の数学と物理が相互に影響し合っているということを身近に感じられた。一方でものごとの理解の仕方には差があるようにも思う。数学の世界で教育を受けてきた私はきちんとした定義がなかったり定理の証明がないとわかった気がしないのだが、物理の人たちは必ずしも完全な証明をしなくても正しい答えを導いてきてその感覚の鋭さに驚かされた。また素粒子物理の研究者である山崎雅人さんと一緒にスーパーリー環についての論文を書く機会もあった：
　Yoshiki Oshima, Masahito Yamazaki, “Determinant formula for parabolic Verma modules of Lie superalgebras”

2013年から9月から2014年7月までの間、カブリIPMUを一旦退職してプリンストン高等研究所に滞在した。プリンストンは大学を中心としたのどかで美しい街だ。研究所の周りでは、あちこちにリスやウサギ、シカを見かけた。何十年も前から変わらないような風景の中で、博士の時にやり残した計算をしながら、自分はこれから何をするべきかを考えていた。

分岐則の問題については博士の時に求めた具体的な公式はあったが、個々に場合分けをして得られたもので、統一的に捉えることはできていない。分岐則を求めることはある意味で自然科学の実験のようなもので、まだいろいろな場合に制限の振る舞いを観察してデータを集めているという段階である。D加群を使って計算した離散分解する場合の他、連続スペクトルを含む場合の分岐則の計算も行った：
　Jan Moellers, Yoshiki Oshima, “Restriction of some unitary representations of O(1,N) to symmetric subgroups”
これらの今までに収集したデータから一般的な構造を理解したいところだが、未だわかっていないことが多い。

[さいごに]

膨大な情報があふれている現代、それらを取捨選択したり、素早く身につけたりということが求められることが多く、一方でひとつのことに時間を贅沢に使って向きあうということは少ないかもしれません。大学院でじっくりと数学を考える経験は、将来数学の道に進むかどうかに関わらず貴重なものになるのではないでしょうか。研究については指導教官と近いことをする必要はなく、自分が興味を持てることをするのが一番であると思います。皆さんと数学をすることを楽しみにしています。