- ホーム
- 講座・教員紹介
- コンピュータ実験数学講座
- 降籏 大介
コンピュータ実験数学講座
教授 降籏 大介 Furihata Daisuke

数値解析スキーム構成研究者です.具体的な手計算が有効な差分法が特に好みです.偏微分方程式の変分構造を保存する離散変分導関数法を提案,今は他研究者も巻き込んで格闘中です.
1968年東京生まれ,長野県で育ちまして,1990年東京大学工学部物理工学科を卒業, 1992年に同大で修士課程を修了後そのまま助教に着任,京都大学数理解析研究所に異動し,2001年に阪大に赴任し,現在に至ります.
研究について
専門は「数値解析による偏微分方程式の求解方法の研究」です.具体的には,連続系である偏微分方程式の解が保持している本質的な性質,特に変分構造を離散系の方程式にマッピングするための方法論です.変分構造による数学的性質を保持するもので,われわれはこれを離散変分導関数法と総称しています.数値的求解が困難な偏微分方程式問題に対してこの方法により初めて実用的な数値的求解が可能になることもあり,実用上も重要な研究です.このように方程式の数学的な構造を離散的に保存する方法を一般に構造保存数値解法(structure-preserving numerical method)や幾何的求積法(geometric integration method)と呼び,偏微分方程式に対してフレームワークとして捉えて研究を始めたのは自分を含む本邦の研究者です.近年ではこの一連の研究は大変国際的なものとなり,このテーマに関する国際研究集会が開催されたり ICIAM や SciCADE など応用数学系の国際学会で大きなセッションを占めるなど,広く知られた分野に成長しています.たとえば 2019年にはイギリスのニュートン研究所でこのテーマのプロジェクトが半年間に渡って行われ,自分も招待されて参加しました.このときの成果はもちろん今に生かされています.


ニュートン研究所の様子.左:居室入り口からホールを見る, 右:自分と他研究者との討論中の黒板
現在は離散的な制限を少しずつ緩和する,より数学的に困難な方向へ研究が進んでいる段階です.例えば空間の離散化の自由度をあげつつ構造保存数値解法の構築することは現在の主な研究テーマの一つで,理論的には空間を任意の凸多角形分割で分割したうえでも構造保存数値解法を構築できるところまで成果を得ています.具体的な例の一つとして空間中に自由に参照点を配置してボロノイ分割という手法で空間を分割することによって数値計算が困難な偏微分方程式の一つであるCahn–Hilliard 方程式に対して二次元数値計算をしたものが下図になります.このように自由度が高いにもかかわらずこの場合は自由エネルギーと呼ばれる積分量が減衰する(これは離散的な変分構造があることに依ります)ことが数学的に証明される,大変優れた解法となっています.
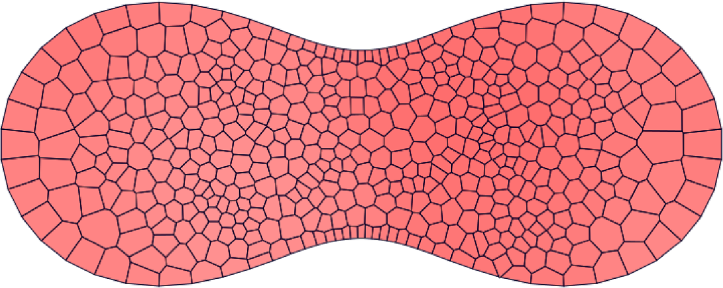
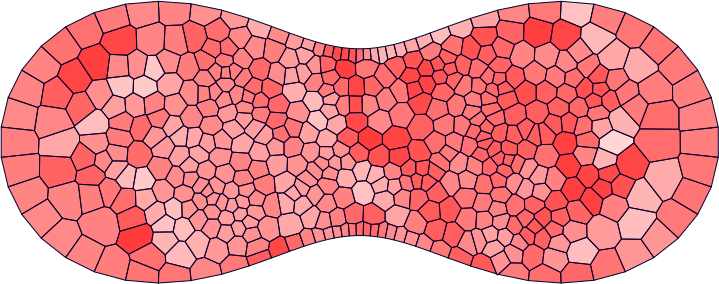
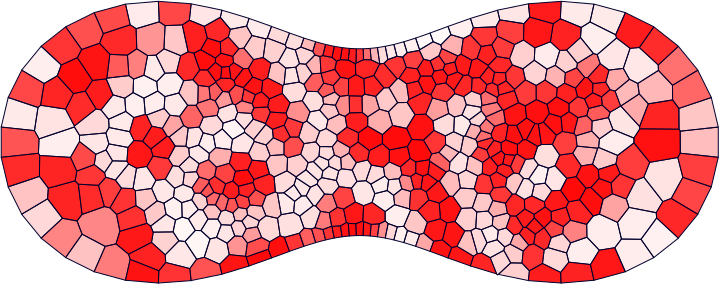
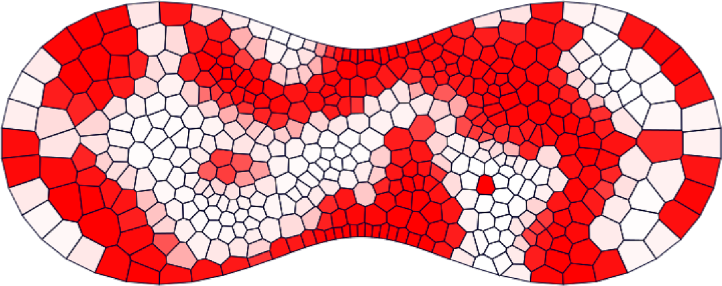
Cahn–Hilliard 方程式の数値解の時間発展の様子.左上,右上,左下,右下へと時間発展していく.ほぼ均一な状態から不均一な状態への変化を表している.
また,離散変分法の基本にある変分の概念やその重要な数学的道具である差分法などを上手に適用することにより,偏微分方程式の数値解法だけではなく,物理現象の新しいモデリングや最適化問題の求解などに面白い結果をもたらすことも可能です.2009年頃までのこうした成果のおおよそは

Discrete Variational Derivative Method,
Daisuke Furihata and Takayasu Matsuo, CRC Press, 2009.
という成書にまとめてありますので,興味がある場合は一読していただけると良いでしょう.
一般の数値解析そのものの話もしておきましょう.この分野は,純粋な数学理論では手のでない問題をコンピュータを用いて具体的に解を得てしまおうという応用数学の一研究分野です.よく誤解されますが,数値解析の難しさは如何に上手なプログラミングを行うかという点にはありません.本質的な困難はもとの連続的な数学問題を有限な離散系に置き換える点にあります.表面的な目的は近似ですが,その本質に一貫した離散数学の裏付けが無いと頼りない成果しか得られないのです.そして,数値解析の歴史は意外に古くて,数学上の重要な定数 $\pi$ や $e$ の数値表現を手計算で求めた歴史も考えれば数学そのものと同じ歴史を持つと言って良いほどのものです.コンピュータの出現によって人類が手にできる計算量と計算速度が圧倒的に増大することでこの数値解析が近年強く意識されるようになってきたのです.ここで,以前行った夏の公開講座「離散と連続 — 微分方程式の数値解析」の abstract を引用しましょう.
数値解析は他の pure math と同じだけの面白さを持っている.
計算機で計算を行う際,実際に計算はどのように行われているのであろうか.ややもすると,計算機ハードウェア自身が数学に関する人類の知識を用いて計算を行う作りになっているかのように錯覚しがちであるが,実はそうではない.計算機ハードウェアは,基本的に四則演算ぐらいの驚くほど単純な計算を受け持つのみである.全ての計算はその単純な計算のみを有限回数だけ用いたアルゴリズムに最終的に還元されて実装されている.つまり,全ての計算が基本的に四則演算の繰り返しだけで実現されていると言ってよい.またメモリの有限性などから,計算機では有理数の一部分のみ,すなわち離散的な数,を用いて通常は計算を行う.
閉じている,という意味で計算機における計算は一つの数学体系をなしているととらえられるが, 上に述べたように,有限かつ離散な計算のみを扱うために結果や方法論が通常の数学とだいぶ異なることになる.素朴な基礎から出発して有限と離散という制限の枠内で何ができるかという命題は興味深いものであり,計算機を背景としてこの命題を研究するのが計算機科学である.つまり,計算機科学は「有限」と「離散」という概念からのみなる数学を研究する分野であると標語的にいいかえてもよいだろう.
計算機科学は,その対象および手法から数値解析と(非数値)情報処理という分野に大きく分けられる.数値解析は関数論等の連続的な数学で記述される問題(数値問題)を扱う分野であり,(非数値)情報処理とは,組合わせ論などの離散的数学で記述される問題(非数値問題)を扱う分野である.数値解析はその性格上,連続と離散,極限(無限)と有限という概念を対応させつつ研究を行う分野であり,情報処理は離散かつ有限という概念を最大限利用して研究を行う分野である.
上記引用からわかるように,数値解析という分野は一般に想像されるよりはるかに奥が深い理論的なもので,また広い範囲におよぶものであることがわかってもらえると思います.
教育について
一般に数値解析だけでなく隣接する離散数学にも自分は興味があり面白いテーマは無いかと日々考察を巡らせていて,指導する学生にも数値解析に限ることなく広い目で応用数学の中から興味あるテーマを選んで研究してもらいたいと思っています.たとえば数値解析ではないテーマの一つとして本学で高校生向けに行った公開講座では応用数学,離散数学の内容を幅広い視点からしってもらうべく「デジタルの数学 — セルオートマトンと計算機」というタイトルで講演を行いました.この講座では,ライフゲームによる具体的なセルオートマトンの性質の提示,UTM(万能チューリングマシン)との関係,「計算」という意味の定義,停止問題によるその限界,物理や数学への応用,自己複製機械などをテーマとしました.こうしたテーマは多くの分野への関連性が強いうえ応用範囲も広いもので,数学の基礎から応用まで縦断する興味深い分野です.自分としては,できればこうした横断的なテーマの研究を行いたいと希望する学生が出てこないかと期待をしているところです.
もう少し具体的な話もしましょう.阪大に赴任してから数学科の 3,4年生などを対象に輪読セミナーや数値解析関連の授業を行っていますが,その際には
「数値計算法の数理」杉原 正顯, 室田 一雄 著, 岩波書店, 1994.
などを主なテキストとしています.数値解析について記した和書のほとんどが紙面の都合からアルゴリズムを紹介するだけに終始してしまうのに対し,この書は数値解析の数学理論的側面を妥協無く記述していて,理論面をきちんと把握したい皆さんには大変ぴったりのものになっています.その分読み解くにはある程度広い分野の数学的素養を要求されますので読み進める際には多少の努力を要しますが,数値解析の面白さと難しさを知るのに非常に良い本と言えましょう.数値解析の本質や理論に少しでも興味のある学生さんには是非とも一読を勧めたい本の一冊です.
また,数値解析が上手に活かされている応用・実用分野について知りたい,研究したいという学生さんが居る場面では
Mathematical Problems in Image Processing, G.~Aubert, P.~Kornprobst, Springer, 2002.
もテキストに使って研究指導をしています.これは画像処理に使われている数学をきちんと考える本で,IT分野で広く使われている画像処理技術を支えるものが偏微分方程式やその数値解析などの応用数学理論などであり,応用数学に携わる研究者の成果が応用につながることを知るのに大変良い教材の一つです.
これまで指導してきた学生さんですが,理学部数学科の4年生と本専攻の修士前記課程学生にわたっておおよそ毎年各学年2名平均というところです.2021年3月には 1名の博士学生が3年間の博士後期課程を修了して無事に博士号を取得し,指導教員として喜んでいるところです.
そして,本専攻の大学院生の指導にあたって自分が最も重視しているポリシーとして「研究テーマ,研究手法の自由度の高さ」と「自主性の尊重」があります.これは学生の皆さんを大人の一人として尊重するものであるとともに,これまで受動的な学習が中心だった学生生活から主体的な学習へと学生さんに行動を切り替えてもらうためにも必要なものと考えています.
また大学院生の指導スケジュールですが,修士1年生は「学習から研究への移行期間」という助走期間とし,修士2年生を「自力による研究の試行期間」と位置づけています. これは,先に述べたように「知識を人から教わる」ことには慣れていても「自分で探る」ことに慣れていない学生の皆さんのために段階的な過程を経て研究の面白さを見いだしてもらいたいためです. 具体的には,修士1年生の間はなるべく自由にテーマを選択してもらいます.例えばこれまでは共役勾配法,非線型問題の求解(Newton法,ホモトピー法など), 二重指数変換積分公式, 有限要素法およびフリーメッシュ法などの数値解析に関するテーマから,線形計画法, 逆問題, 機械学習, 制御問題,結婚問題や選曲割問題などの離散数学による社会問題への応用まで,応用数学の幅広い多くのテーマが学生自身によって選ばれています. そして,論文ならびに書籍を資料として学習し,コンピュータでプログラミングを行って追実験を行い,様々な比較検討および評価を行った結果をセミナー形式で発表して,そのテーマにある程度通暁した時点で再び他のテーマを選び,同様の過程を繰り返していくという格好です.この際,研究への移行という位置づけから,テーマの選択から発表まで全体を通して自力で行えるようになることを重要な目的としています.
修士2年生では2~4ヶ月という比較的長い期間を用いて,研究テーマを自力で試行錯誤しながら探すことから始めてもらっています.
自分でテーマを決めることは皆さん初めてなのですが,テーマを探すために下調べをすること自体が学習に大変有効なのです.
例えば,これまでは走化性方程式系,非線形格子上の離散ブリーザ─, Allen-Cahn 方程式, 正規化長波長波動方程式,拡張 Fischer-Kolmogorov 方程式, Swft-Hohenberg 方程式などの非線形偏微分方程式の離散化に伴う問題やその数値解の解析を始め,種々のテーマが修士論文のために学生さん自身によって選ばれています.テーマを決定した後は研究に邁進することになります.具体的には修士学生のセミナーで現状報告を行い,何が問題なのかを常に整理して研究の方向を適切に修正するように指導を行っています.この際,方法論やおおまかな方向についてはなるべく詳細に指導を行いますが,作業や考察,問題の提議等はできるだけ自力で行えるように示唆しています.これは学生さんの自主性を損なわないようにというものですから,皆さん,自分のペースで進めてくれれば良いと思います.そして研究の成果が得られ始めた時点で学会や研究集会で研究成果を学生さんに発表してもらっています.こうすることで,自分の研究がどのような位置づけにあるのかを総合的に実感をもって理解することができるでしょう.
そして近年,同じ研究室に優秀な若手准教授である宮武准教授を迎えたこともあり,学生を受け持つ教官として,特に大学院生の指導教官として指導内容により新しい内容を加え,なるべく最先端の研究内容に沿うような指導を行ってゆきたいと考えています.そのため,どのような方向に向かって学生と研究を行うかは,実際に学生の意思や自主性を意図的に重要視し,生かしていこうと努力しています.繰り返しになりますが,学習・研究のスタイルでも内容でも学生の自由度は高い研究室ですから,自主性を強く持ちたいと願っている学生さんは特に歓迎します.ぜひ参加してください.
略歴
- 1992年 東京大学 工学部 物理工学科 助手
- 1997年 東京大学 博士(工学)
- 1997年 京都大学 数理解析研究所 助手
- 2001年 大阪大学 サイバーメディアセンター 講師
- 2002年 大阪大学 サイバーメディアセンター 助教授 (准教授に職名変更)
- 2017年 大阪大学 サイバーメディアセンター 教授
連絡先
4ケタの電話番号は、大阪大学での内線番号です。
メールアドレスは、末尾の"osaka-u.ac.jp"が省略されていますので、送信前に"osaka-u.ac.jp"を付加してください。



